Lost and Found: How GPS Triangulation Pinpoints Your Spot

Have you ever been completely turned around in an unfamiliar place, only to pull out your phone and instantly see exactly where you are on a map? It feels like magic, right? One moment you're adrift, the next, you're precisely located on a digital canvas. But what invisible forces are at play to make this seemingly effortless act possible? The secret lies in a brilliant piece of technology called the Global Positioning System (GPS), and specifically, in a clever geometric technique that's often simplified to 'triangulation'.

Table of Contents

What is GPS, Anyway? More Than Just an App on Your Phone

Before we dive into the how, let's quickly define the what. GPS isn't just a feature on your phone; it's a global navigation satellite system (GNSS) maintained by the United States government. It consists of three main parts:

Space Segment: A constellation of orbiting satellites (currently 31 operational satellites in orbit).
Control Segment: Ground stations that monitor and maintain the satellites.
User Segment: The GPS receivers in your devices (phones, car navigators, smartwatches, etc.) that pick up the satellite signals.

It's the interaction between the space segment and your user segment receiver that allows you to figure out where you are.

The Whispers From Space: Satellite Signals

Way up in space, these satellites aren't just passive observers; they're constantly broadcasting radio signals down towards Earth. Each signal contains crucial information:

The satellite's precise location in orbit (ephemeris data).
The exact time the signal was sent (using incredibly accurate atomic clocks).

Your GPS receiver is designed to pick up these faint signals from multiple satellites simultaneously.

Illustration of GPS satellites orbiting Earth and sending radio signals down to a receiver on the surface. — GPS satellites constantly broadcast signals containing their location and precise time.

Measuring the Journey: From Time to Distance (Pseudorange)

This is where the magic begins. Your GPS receiver listens for the signals from multiple satellites. By comparing the exact time the signal was sent (included in the signal data) with the exact time it was received, your device can calculate how long the signal took to travel from the satellite to you.

Since radio waves travel at the speed of light (roughly 186,000 miles or 300,000 kilometers per second), we can use a simple formula:

Distance = Speed × Time

So, by multiplying the signal's travel time by the speed of light, your receiver calculates its distance from each satellite it can 'see'. This calculated distance is often called a 'pseudorange' because, as we'll see, it's not a perfectly accurate distance yet due to tiny errors in the receiver's clock compared to the satellite's atomic clock.

The Geometry Game: Intersecting Spheres

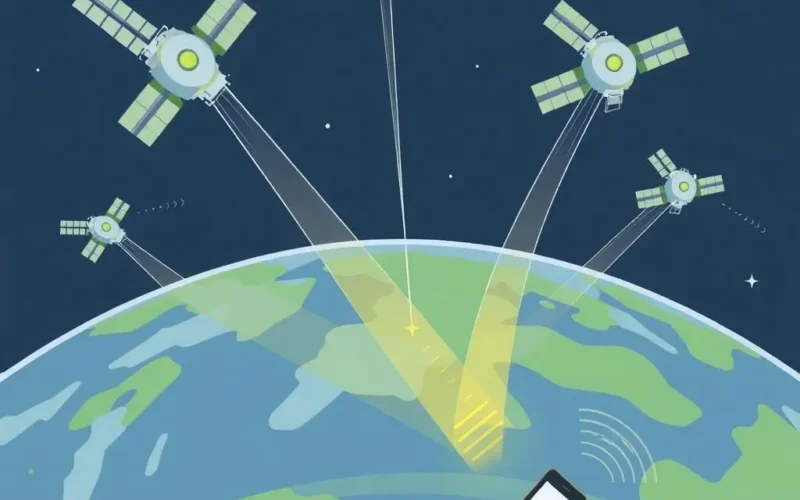
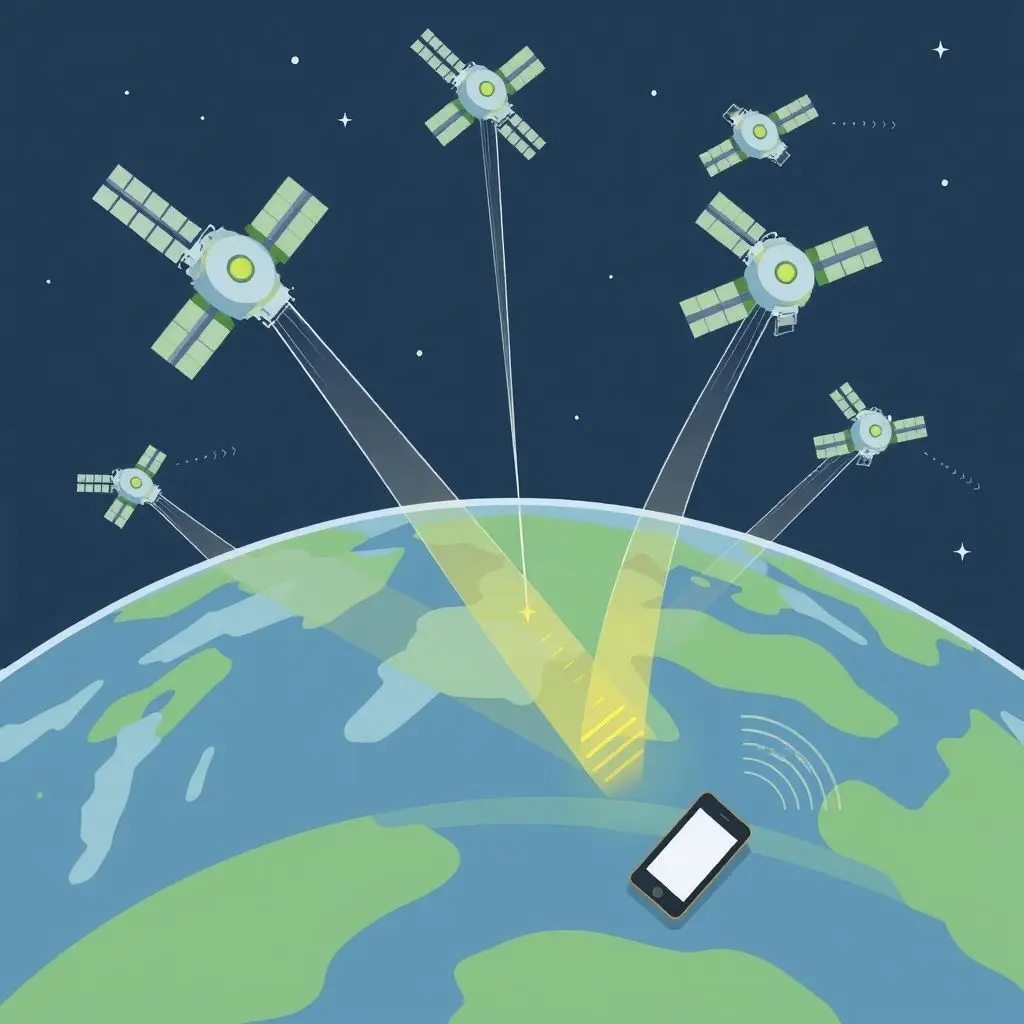
Imagine you know your exact distance from a single point in space (a satellite). Where could you possibly be? You could be anywhere on the surface of a giant, invisible sphere centered on that satellite, with a radius equal to the calculated distance.

Okay, one sphere gives us way too many possibilities. What if you know your distance from a second satellite? Now you have two spheres. The intersection of two spheres in 3D space isn't a single point; it's a circle.

Still not pinpointed! But what happens when you add a third satellite? You now have three spheres. The intersection of three spheres narrows down your possible location dramatically. If your receiver's clock were perfectly synchronized with the satellites' atomic clocks, the intersection of these three spheres would result in just two potential points in space.

Visualization showing three spheres intersecting at two distinct points. — The intersection of three spheres gives two possible locations.

One of these points is usually easily discarded because it's in an utterly improbable location (like thousands of miles above Earth, or far off in space). This leaves one likely position. This is the core geometric principle behind GPS positioning – finding the point where spheres of known radii (the distances from satellites) intersect.

This process is often referred to as 'triangulation' or, more accurately, 'trilateration', which specifically refers to determining a position based on distances from multiple known points.

Why Four is Better (and Often Necessary)

If three satellites give us a location, why do GPS receivers ideally use signals from four or more? Remember that 'pseudorange' we talked about? The calculation relies on knowing the exact time the signal was received. While satellite clocks are incredibly precise, the clock inside your phone or GPS unit isn't. This small error in your receiver's clock leads to an error in the calculated travel time, and therefore, an error in the calculated distance (the pseudorange).

This clock error introduces uncertainty. To solve for your precise 3D location (latitude, longitude, and altitude) *and* solve for the receiver's clock error, the system needs to solve for four unknowns. This requires measurements from at least four satellites. The fourth satellite adds another equation, allowing the receiver to calculate not just its position, but also the necessary correction to its internal clock.

Visualization showing four spheres intersecting at a single, precise point, representing a GPS receiver's location. — A fourth satellite helps correct for receiver clock errors and pinpoint a more accurate location.

Using more than four satellites further improves accuracy and reliability, helping to filter out noise and mitigate other errors.

Want a quick visual walkthrough of this intersection concept? Check out this short video explaining the core idea:

Beyond the Basics: Factors Affecting Accuracy

While the sphere intersection model is the fundamental principle, real-world GPS isn't always perfectly precise. Several factors can introduce errors and affect how accurately your location is pinpointed:

Atmospheric Delay: Signals slow down slightly as they pass through the Earth's ionosphere and troposphere. This effect can vary depending on atmospheric conditions.
Multipath: Signals can bounce off buildings, mountains, or other objects before reaching your receiver. This makes the signal travel a longer path, tricking the receiver into thinking it's farther away from the satellite than it is.
Satellite Geometry (DOP): The relative positions of the satellites in the sky affect accuracy. If the satellites are clustered together, the intersection of the spheres is less well-defined. If they are spread out (good geometry), the fix is more accurate. This is measured by something called Dilution of Precision (DOP).
Ephemeris/Clock Errors: Although minimal, slight errors can exist in the broadcast information about the satellite's exact position or time.
Receiver Quality: The quality and sensitivity of your GPS receiver hardware and software play a role.

Illustration showing a GPS signal bouncing off buildings before reaching a receiver, causing a multipath error. — Obstacles like buildings can cause multipath errors, affecting GPS accuracy.

Modern GPS receivers use sophisticated algorithms and signals from multiple GNSS systems (like Russia's GLONASS, Europe's Galileo, and China's BeiDou) to mitigate these errors and provide highly accurate positioning.

Frequently Asked Questions About GPS Pinpointing

Let's clear up a few common questions:

Q: Do I need an internet connection for GPS to work?
A: No, the core GPS function (receiving satellite signals to calculate position) does not require internet. However, mapping apps that display your location on a map *do* require map data, which often comes from the internet. Assisted GPS (A-GPS) uses cellular or Wi-Fi data to quickly get initial satellite information, speeding up the first fix, but it's not strictly necessary for basic operation.

Q: What happens if I only see 3 satellites?
A: If you only have a clear view of three satellites, a receiver can potentially calculate a 2D position (latitude and longitude) if it assumes a fixed altitude (like sea level). However, it cannot solve for altitude or correct for the receiver's clock error without a fourth satellite, making the 2D fix less accurate.

Q: Does weather affect GPS accuracy?
A: Heavy rain, snow, or dense clouds can sometimes slightly attenuate (weaken) the GPS signals, making it harder for the receiver to lock onto enough satellites. However, moderate weather typically doesn't prevent a fix. Severe atmospheric disturbances can increase atmospheric delay errors.

Q: Is GPS triangulation the same as cell tower triangulation?
A: No, they are different. GPS relies on signals from satellites in space and the calculation of distances via signal travel time. Cell tower triangulation (or more accurately, trilateration using signal strength or timing) uses signals from nearby cellular towers on the ground to estimate your location, which is generally less accurate than GPS.

An Invisible Network Guiding Our Way

The next time your phone instantly shows you where you are, take a moment to appreciate the intricate dance happening high above the Earth. Tiny whispers from orbiting satellites, traveling at the speed of light, are being captured and measured by your device. Through a clever application of geometry and precise timing, these signals intersect in virtual spheres, allowing your receiver to calculate its distance from multiple points and ultimately pinpoint your location on our planet.

It's a testament to human ingenuity and the power of physics and mathematics, enabling everything from navigation and mapping to precision agriculture and disaster relief. This invisible network is constantly at work, quietly guiding us through our modern world.